
👾 Game Master
6/21/2022, 7:57:07 AM
Present Value (PV) and Net Present Value (NPV)
Introduction
In finance, the valuation of an asset, including stocks, bonds, commodities, and options, lies at the core of trading. The value varies from day to day, and the majority of the finance world agrees that the present “value” of money (AKA the intrinsic value) is worth more than the future “value”. Such principle is called the Time Value of Money (TVM). The Time Value of Money is fundamental for many financial concepts, including the calculation of present value (PV) and net present value (NPV).
Present Value of Asset
To address the calculation of PV, let’s start with a math problem.
- Alex saves $1000 in his bank account. The account is compounded on a yearly base with an annual interest rate of 10%. What value Alex is expecting to get after saving the money for 5 years?
According to the calculation of compound interest, five years later, Alex’s account will worth:
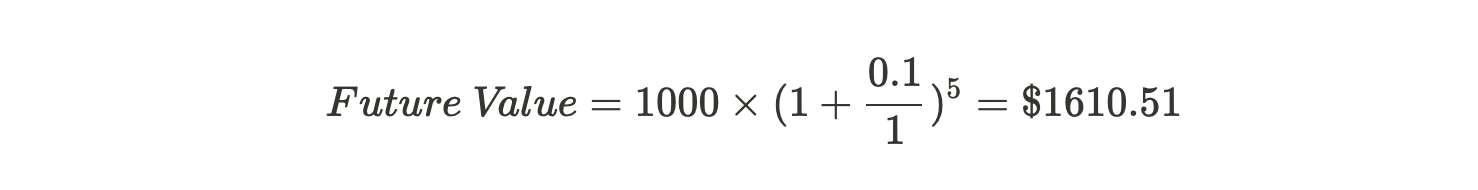
If we change the scenario into a stock account instead, the calculation also stands. Here, the interest rate will become the return rate of the stock account.
Now, what if instead of knowing the current value (which is the $1000 in the example above), we know the future value? We then need to twist the formula a bit:
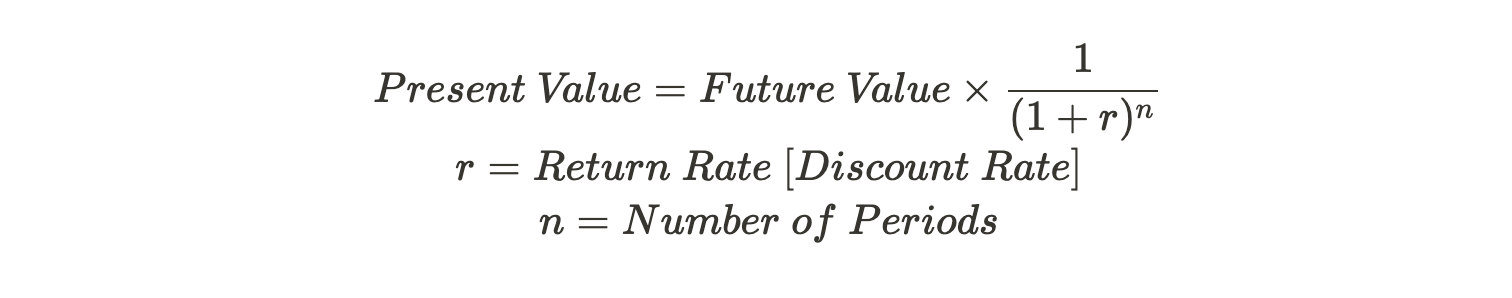
Discount Rate
As we now understand that money today is worth more than money in the future When calculating the present value of an asset back from its future value, we generally call the theoretical opportunity cost of capital, or the ideal “interest rate/return rate” the discount rate.
Risk, return. Two highly correlated terms in finance. According to most financial markets, higher returns generally mean taking more risks (the alternative also stands, i.e. taking more risks can generate more “potential returns”). Therefore, the higher the risk, the higher the discount rate.
A key thing to notice is that in the real world, it is nearly impossible for any investor to predict the future value accurately. Therefore, the discount rates that we are using in the calculation are either “theoretical” or “relative.”
There are financial theories that can provide a potential discount rate for an asset, such as the Weighted Average Cost of Capital (WACC), which is a theoretical discount rate for a company’s future free cash flow.
The term is also linked to the basic concept of opportunity cost. Opportunity cost is the potential return given by an alternative or similar investment. There are some investments in the market, such as a bond or bank deposits, that offer known return/discount rates. By using these rates in the calculation of PV, it represents the highest money that the investor should accept. If the asking price is higher than the present value, the other investments might be more optimal choices.
- Present Value is the discounted value of future returns. It reflects the intrinsic value of a deal, AKA the “real value”. Net present value is the present value plus the costs (negative value), in another word, the present value of cash inflows minus cash outflows.
Example & Calculation
A simple & organized way to manipulate PV calculation is through excel. Embedded formulas in Excel are efficient in deriving PV. Here is an example:
- Avril is investing in an investment that promises $100 in return every year for the future 5 years. An alternative asset management plan for Avril is to save her money in the bank, which offers a 10% annual interest rate for 5 years.
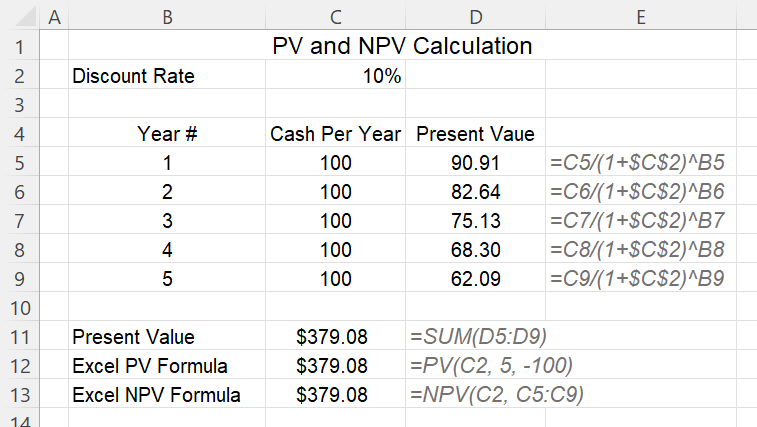
Now, let’s assume that the investment above is sold for $400 dollar. Will that be a worth it investment? For people who didn’t learn the time value of money and PV & NPV, they will accept the deal because... $$100\times 5$ is far greater than $400. But ... Is that really the case?
The calculation we did above suggests that taking into consideration of opportunity cost (the 10% interest offered by the bank), the investment is only worth $379.08. Therefore, any price over this should not be an acceptable deal.