Prediction Model: What is the Challenge?

After computer and modeling technologies are popularized, using financial models to predict future market returns had become a topic that gathered many experts and institutions’ attention. But the process to forecast future market trend is often challenging. Let’s take the stock market as an example. Over 56% of US adults are investing in the stock market. With millions of participants competing for their target prices, the stock market is filled with countless influencing factors that can affect the future price. Accordingly, the difficulty of accurately modeling the stock market increases.

Solution: Randomness

Fama introduced the Efficient Market Hypothesis (EMH) in his book Efficient Capital Markets: A Review of Theory and Empirical Work. This is an evolutionary step in financial modeling since it provides a new lens for describing all the trivial market-determining factors — through a random process. In brief, the short-term fluctuation in stock prices can be described as multiple random processes of variables, which is called the Random Walk.

An example of a Random Walk is shown below. It is not hard to see that there are countless possible factor scenarios that affect price, since the trend is “randomly” determined.

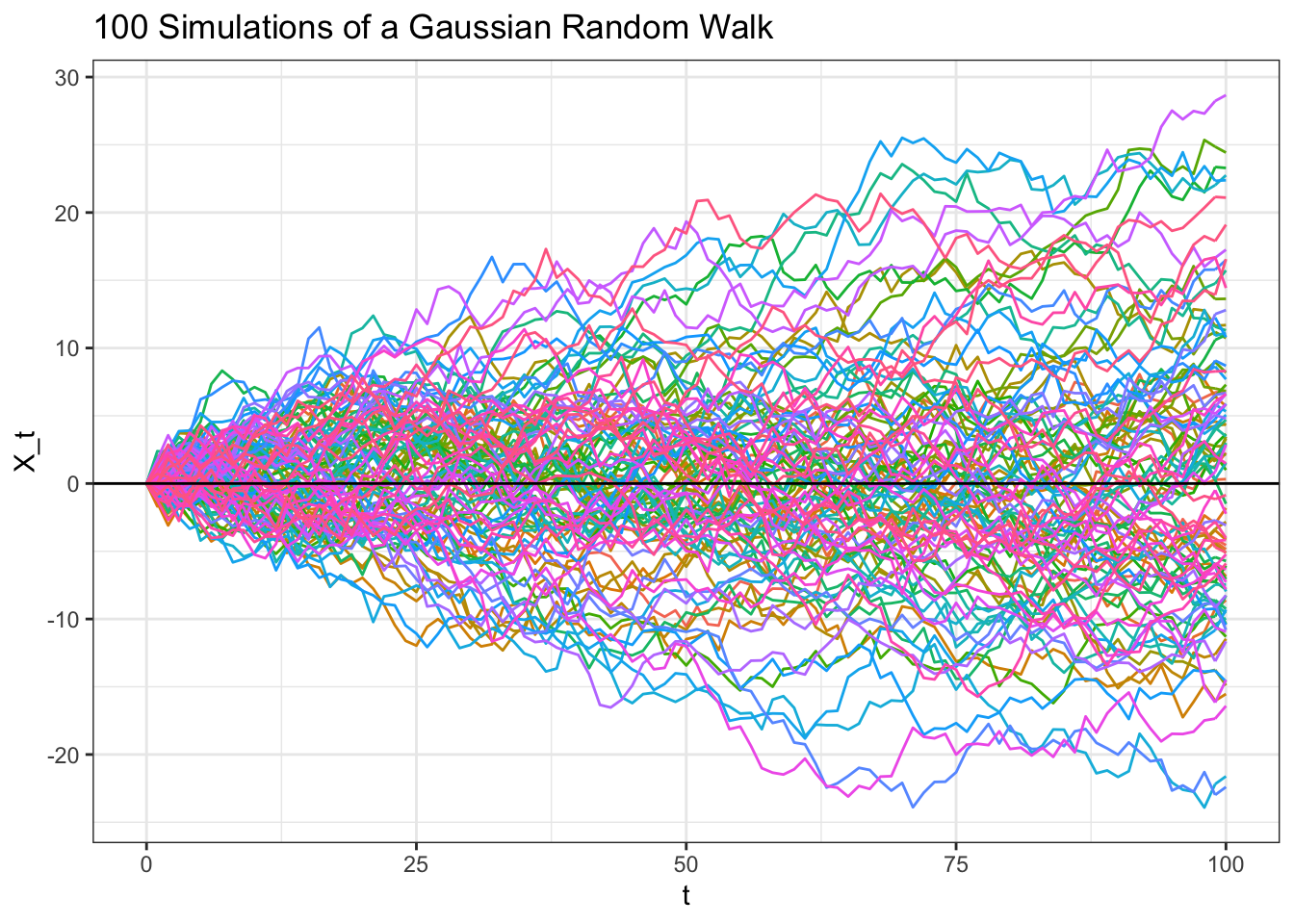
Therefore, in many modern finance models, people can use computers to describe factors that they are capable of explaining, and summarize all the trivial factors by a so-called “random variable.”

Monte-Carlo Simulation: What is its Role?

Now, we have the ability to summarize the market trend. Yet, just like the graph above suggests, the existence of random variables outputs many different outcomes. Therefore, it is not correct to select one result, since there are potentially many other outcomes.

The Monte-Carlo Simulation simplifies the randomness issue. This method requires people to run the random process on a large number of trials (for LARGE I mean 10,000+). Once the process is complete, the average of all potential results can be taken to derive an aggregate estimation.