Risk and Return

The stock market is filled with countless factors. Some are qualitative (such as important news, new product release, or market sentiment), and some are quantitative (AKA can be expressed using numbers). It is essential to learn the tricks to play around with the numbers in quantitative finance.

The key goal of an investment is to make money and generate returns. The Modern Portfolio Theory states a relation between return and risk. According to this theory, the target for investors is to maximize the return of an investment portfolio while minimizing the risks. By doing so, we can then construct the so-called efficient portfolio.

In this article, we will learn three important mathematical concepts that can help us tackle the risk-return problem. Mean is an indicator for return, and variance and covariance are a pair of indicators for risks. Two additional mathematical indicators for risk are presented in the article Standard Deviation and Correlation.

Image source: https://time.com/nextadvisor/wp-content/uploads/2021/09/na-what-are-cyclical-stocks.jpg

1. Mean

There are some other names for mean, such as “average value” and “expectation (a more narrowed down type of mean and will be mentioned later).” The calculation of the mean is simple. All we have to do is to take the sum of all data and divide it by the total number of data. To demonstrate it in a mathematical expression, the formula is like this:

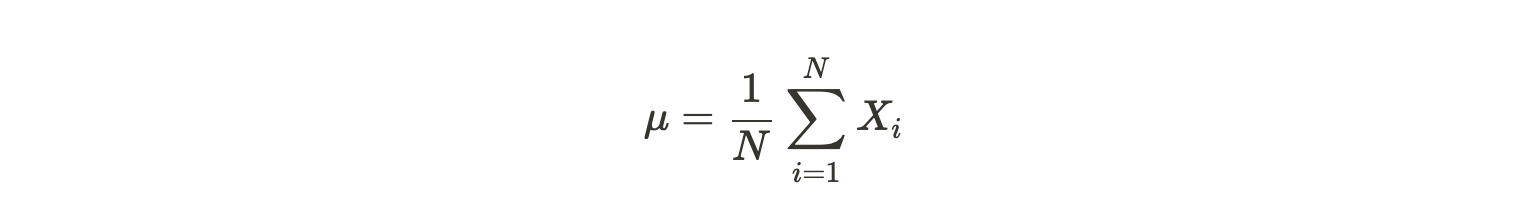
Here, µ is the notation in math for “mean.” N stands for the total number of data samples, and Xi is the value for each data in a sample.

Σ notation stands for taking all the sum of.

Expected Value

We generally focus on a more narrowed type of mean in finance, called expectation. The expected value is equivalent to the “weighted average,” which means the average that considers the proportion for each data sample. We use expected value in a portfolio because we generally invest a different amount of money into different stocks. Thus, it is biased if we treat the return of each stock similarly. To be more objective, an effective way is to multiple the returns by their “weight”:

The result that we derived will then be the “expected return” for a given portfolio.

CAPM Formula

It is worth noticing that another approach to calculating the “expected return” of an asset is through the The Capital Asset Pricing Model (CAPM) formula. Both the CAPM formula and the formula we introduced above are commonly used in models, and they are both effective depending on the scenario.

2. Variance

To quantify “risk,” we need to know how spread out the sample values are from the mean. A variance is a good tool in this case. According to the formula, variance is the “mean” of the distance for each sample points to the mean value.

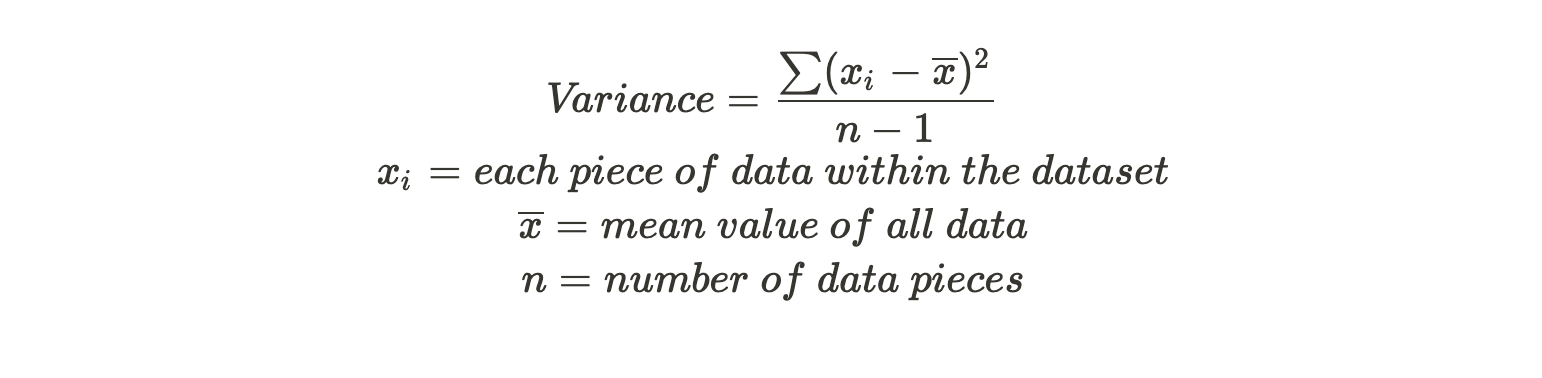
Standard Deviation

Depending on the background, some investors prefer to use standard deviation in measuring the risk. Standard deviation is simply the square root of variance. To learn more about standard deviation, check out the article Standard Deviation and Correlation.

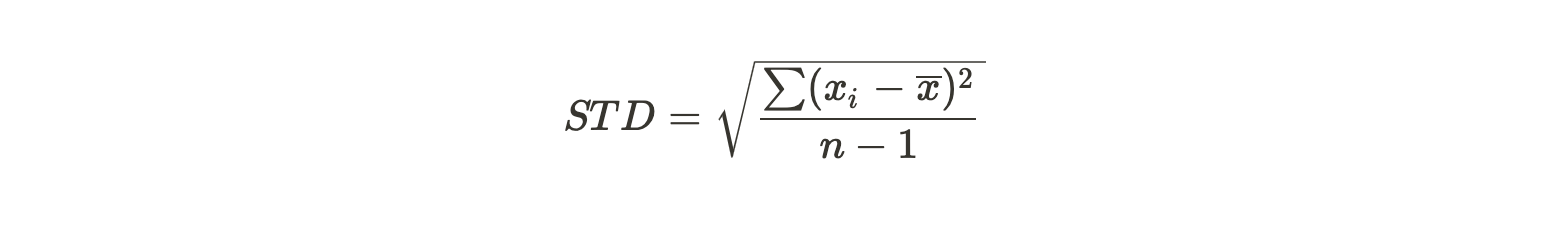
3. Covariance

Using mean and variance, we now successfully quantified the expected return of a portfolio and the risk of a given stock within the portfolio. One thing left that we need to work on is the risk of the entire portfolio. To do so, we need first to derive the risk of an asset with respect to another asset. Assets, in general, are often dependent on each other, with different covariance numbers reflecting the interconnectedness of different asset classes. The covariance is a handy tool because it estimates the relationship between the two assets.

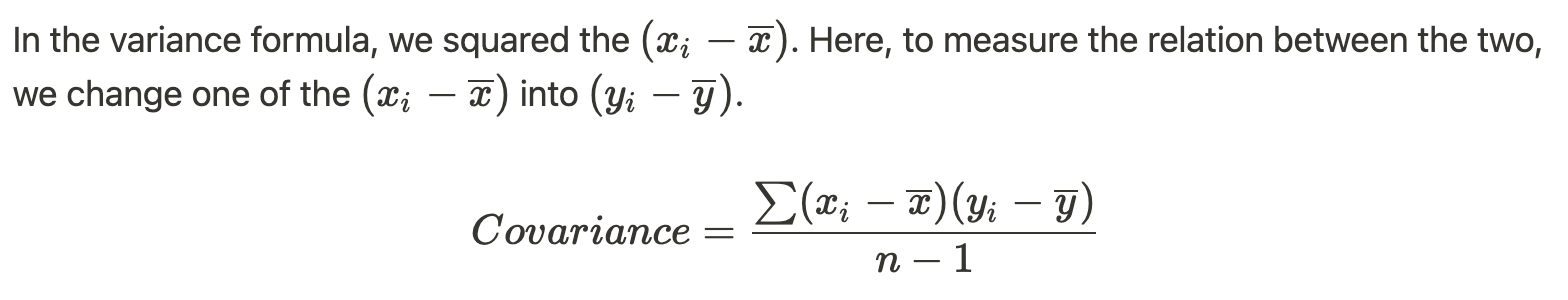
A positive covariance means that a smaller x will be very like associated with a larger y (and the opposite also stands).

Variance-Covariance Matrix

A variance-covariance matrix is a handy tool to assess the risk of an entire portfolio. To derive this matrix, we need to implement both the variance and covariance calculations that we just learned above. A variance-covariance matrix contains all covariance of assets with respect to all other assets in a portfolio.